例題14-3:numpyで楽々¶
A: さて、それでは例題14-2の続きだ。本当は一気に例題14-4まで書くつもりだったんだが、この時期(1月~2月)忙しいもんだからずいぶん間が空いてしまった。 「正直なところ自分でも何を書くつもりだったか覚えてないからネタをちゃんと消化できるか自信がない とかなんとか作者が言ってたぞ。
B: いきなり不安なすべり出しですね。大丈夫ですか?
A: まあ作者はもともとアレな奴だからな。俺らががんばるしかないでしょ。というわけでさっそく本題。
B: 無駄話してる余裕すらないんですね…
1import os
2import os.path
3import pylab
4
5cndList = ['E1-MRot','E2-MRot','E3-MRot','E4-MRot','E5-MRot','E6-MRot']
6nCnd = len(cndList)
7nLR = 2
8nPB = 2
9nDIR = 4
10
11L = 0
12R = 1
13NA = 2
14B = 0
15P = 1
16
17LRList = [L,R]
18PBList = [B,P]
19DIRList = [0, 90, 180, 270]
20
21reactionTime = []
22
23for (root, dirs, files) in os.walk(os.getcwdu()):
24 if root == os.getcwdu():
25 continue
26 tmpReactionTime = pylab.zeros((2,2,4,6))
27 for f in files:
28 r,e = os.path.splitext(f)
29 if e.lower() == '.txt':
30 fp = open(os.path.join(root,f),'r')
31 line = fp.readline()
32 for i in range(nCnd):
33 if line.find(cndList[i])>=0:
34 cndidx = i
35 break
36
37 tmpData = pylab.zeros((96,5))
38 idx = 0
39 for line in fp:
40 data = line.rstrip().split(',')
41 if data[0]=='L':
42 tmpData[idx,0] = L
43 else:
44 tmpData[idx,0] = R
45 if data[1]=='B':
46 tmpData[idx,1] = B
47 else:
48 tmpData[idx,1] = P
49 tmpData[idx,2] = int(data[2])
50 tmpData[idx,3] = float(data[3])
51 if data[4]=='L':
52 tmpData[idx,4] = L
53 elif data[4]=='R':
54 tmpData[idx,4] = R
55 else:
56 tmpData[idx,4] = NA
57
58 idx += 1
59
60 fp.close()
61
62 correct = tmpData[:,0]==tmpData[:,4]
63
64 for i in range(nLR):
65 for j in range(nPB):
66 for k in range(nDIR):
67 tmpReactionTime[i,j,k,cndidx] = \
68 pylab.mean(tmpData[correct & (tmpData[:,0]==LRList[i]) & \
69 (tmpData[:,1]==PBList[j]) & (tmpData[:,2]==DIRList[k]),3])
70
71 reactionTime.append(tmpReactionTime)
72
73reactionTime = pylab.array(reactionTime)
74
75LRLabel = ['L','R']
76PBLabel = ['B','P']
77
78for i in range(nLR):
79 for j in range(nPB):
80 pylab.subplot(2,2,2*i+j+1)
81 for k in range(nCnd):
82 pylab.errorbar(pylab.arange(nDIR)+0.02*k, \
83 pylab.mean(reactionTime[:,i,j,:,k],0), \
84 pylab.std(reactionTime[:,i,j,:,k],0,ddof=1), \
85 label=cndList[k],fmt='o-')
86 pylab.title('Hand: '+LRLabel[i]+' / SIDE: '+PBLabel[j])
87 pylab.xticks(pylab.arange(nDIR),DIRList)
88 pylab.legend(loc='upper left')
89
90pylab.show()
A: さて、続けて読んでくださっている方は例題14-2の最後を覚えておられると思いますが アホな作者のために振り返っておきますと 、例題14-2では「刺激が右手か左手か(2水準)」×「刺激が手の甲か手のひらか(2水準)」×「刺激の回転角(4水準)」×「実験条件(参加者の姿勢:6水準)」のデータを整理して、横軸を回転角として、残りの要因の全ての組み合わせの折れ線グラフを描こうとしていました。で、B君が例題14-2の方法でデータを整理しようとして敢え無く撃沈。例題14-2の方法でやれないことはありませんが、データが複雑で私なら絶対やりたくないなあって言ったところで終わったわけです。
B: ホントにひどい人っすよね、Aさん。
A: (無視して) で、私ならどうするかというと、例えばこの14-3a.pyのようにするかなあ、ということで。20行目までのちょっとした気配りにも注意してほしいところだけど、今回のサンプルの前半の山場は26行目、67から69行目、71行目、73行目。26行目にあるように、numpy.zerosの引数には要素数3以上のタプルを与えることができる。それによって3次元以上のnumpy.ndarrayを作ることが出来る。
B: 3次元の、配列?
A: そういえば配列という言葉をきちんと説明したことがなかったな。C言語やBasicとかの頃は基本中の基本だったんだが、pythonではリストが基本だからな。 簡単に言えば、配列とはデータをずらっと並べたものだ。まあ「データを並べた」というだけならリストもそうなんだが、整然と並んでいるところがリストと異なる。…あー。うまく言えないな。
B: 整然と?
A: 百聞は一見に如かず。実例を見てみようか。numpy.zeros((2,3,5))としてnumpy.ndarray型のインスタンスを生成すると、以下のようなデータ構造が構築される。
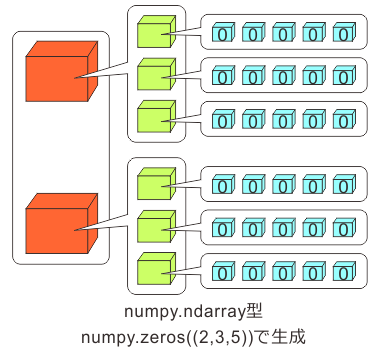
A: 左から見ても右から見てもいいんだが、左から見ると、まず大きな赤い箱が2つある。これらの箱にはそれぞれ3つの緑の箱が入っている。 そして、緑の箱にはそれぞれ青い箱が5つずつ。入っている。これらの構造がnumpy.zerosの引数に与えた(2,3,5)というタプルに対応している。 そして、青い箱には0という値が1つずつ格納されている。青い箱には別の箱を入れることは出来ない。
B: ぼくにはそれぞれオレンジ、黄緑、水色の箱に見えますが…
A: うるさい。とにかくポイントは、 それぞれの色の箱には何が何個入っているかが決まっている ということだ。これがさっき「整然と並んでいる」と言ったことの意味だ。
B: なるほど。ところで水色の箱には0しか入れられないんですか?
A: numpy.zeros()が「すべての要素が0の配列を生成する」という関数だから0が入っているだけのことで、スカラー値なら何でも代入できる。
B: スカラーってベクトルじゃないやつですよね。
A: ぐ、微妙な表現だな…まあいい。データを並べる方法としてもうひとつ リスト と呼ばれるデータ構造があるんだが、リストでは箱がバラバラに散らばっていて、それぞれの箱には「次の箱はアレ」、「前の箱はソレ」といった順番が記されている。 これに比べたらnumpy.ndarrayは「整然と並んでいる」だろ?
B: 確かに。
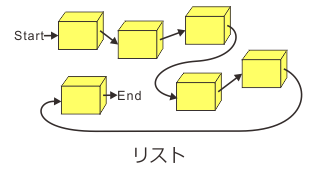
A: リストは配列と違って箱がバラバラに散らばっているので、「先頭から2500番目の箱」といった具合に番号を指定してアクセスするのが大変だ。先頭から順番にたどっていかなければならない。
B: 2500番目って、2500個もずーっとたどっていくんですか?
A: もちろんそういうことになるな。
B: ぐは、なんでそんな無駄なことを。
A: 並べられたデータに対して「253番目」、「3番目」、「827番目」、…といった具合に不規則な順番にアクセスすることをランダムアクセスというが、ランダムアクセスはリスト型が苦手とする処理だ。 一方、リスト型の方が有利な処理もある。典型的なのはデータの並びの途中に新しいデータを追加したり、途中のデータを一部削除したりといった処理だ。 リストならちょいちょいと「前の箱」、「次の箱」を書き直してやるだけで済むが、配列にはこういう柔軟さがないので大がかりな操作が必要になる。
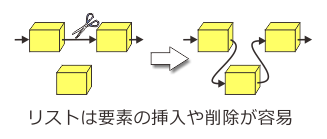
B: うーん、わかるような、わからないような。
A: C言語とかで長さが変化するデータを扱うプログラムを書いたことがある人はこのありがたみがよくわかると思うよ。 ところでリストの絵には箱に何も書いていないけど、どういう意味かわかるか?
B: へ? 意味あるんですか? Aさんのことだから単に面倒くさくて何も書いてないだけかと思ってましたが。
A: む。面倒くさがりは否定しないが、ここでは意図的に空白にしてある。リストにはいろいろな実装方法があるので一概には言えないんだが、リストの「箱」の中には何も入っていなくて、「箱の中身は××に置いてあります」というメモ用紙だけが入っている。
B: ええっ、なんじゃそりゃ!
A: こうしておくといいこともあるんだよ。さっきのnumpy.ndarrayの例では最後の青い箱にはひとつの数値しか入れることができなかった。 しかし、「中身はここにあるよ」というメモ、正確に言うと 参照 を入れることにしておけば、大きいデータでも小さいデータでもお構いなしにひとつのリストとして並べることができる。 例えばリストの箱に「別のリストの先頭がここにあるよ」という参照を入れておけば、多次元のリストを作ることができる。例題1-3で[1,2,[100,200,300],4,[400,500]]というリストが出てきたが、こんな具合に全然型の違うデータをほいほいまとめることができるのはリストならではだ。
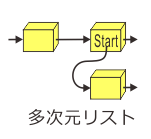
B: ふむふむ。なんとなくリストの良さがわかってきたぞ。でも例題1-3とはまた懐かしいものが。参照っていう言葉もどこかで聞いたような…。
A: 例題5-2 のことかな。関数の引数の値渡しと参照渡しの話をした時だな。 ちなみに 参照の配列 というものを使うと、配列でもこういった柔軟なデータ構造を作ることができるんだが、どんどん今回の例題の目的から逸脱していっているような気がするのでこれ以上は踏み込まないでおこう。だいたいでいいので配列というもののイメージをつかんでもらえたら脱線した甲斐があったかな。 というわけで67行目だが…
B: ちょっと待ってください。pythonの[ ]で作るデータはリストなんですよね?
A: ん? a = [3,2,5,6,2,-1,0,6,5]とかで作る奴か? 確かにList型だがそれが何か?
B: じゃあ今までa[7]とかやっていた時には、いちいち先頭から7番目までたどっていたですか?
A: あー。相変わらず痛いところを聞いてくるな。以前ちょっと調べたことがあるんだが、どうやらpythonの内部ではList型は上記の説明でいうところの「配列」に近い実装になっているらしい。 ただ、私が自分でちゃんと確認したわけではないので、ここではあくまで「らしい」ということで勘弁してくれ。
B: えー。
A: あまり資料がないので最悪pythonのソースを読まにゃならん。そんな時間あるかいな。動きゃいいんだよ、動きゃ。
B: うわ、逆切れだ。
A: うるさい。先に進むぞ。26行目で4次元のnumpy.ndarray型配列を確保したので、67行目での平均値の計算結果の格納先の記述はとっても簡単になる。単にtmpReactionTime[i,j,k,cndidx]と書けばいい。
B: ええと、i,j,kってのは…
A: それぞれ「右手か左手か」、「手の甲か手の平か」、「回転角度」の値が入る。で、71行目のようにリストにどんどん放り込む。
B: ここでリストが出てくるんですか?
A: この例題14では実験参加者数が増えてもプログラムを書き換えずに対応できることを前提としている。何人分のデータがあるかわからない時にはリストにどんどんappendしていくほうが楽だ。適所適材だな。
B: なるほど。
A: で、73行目。参加者別の処理が終わってグラフ描画に入る第一段階だが、ここが個人的にnumpyを初めて触った時に感心したところ。4次元のnumpy.ndarray型のデータを20個を並べたリストをnumpy.array()に渡してnumpy.ndarray型に変換すると、きちんと最初の次元の要素数が20の5次元のnumpy.ndarray型データが得られる。
B: ???
A: 要するにもとは(2,2,4,6)の4次元のデータを20個並べたものだったのが、(20,2,2,4,6)の5次元になるということ。
B: …なんだか当たり前のように聞こえますが。
A: 当たり前だと思うことを当たり前のように実行できるというのはとても素晴らしいこと だよ。プログラミングなんて「なんでこう書けないんだよ!」って文句をつけたいことの連続だからな。
B: あー。それは納得。
A: さて、準備ができたところでグラフを描くわけだが、ここで前回からB君にいじめられているpylab.subplot()が出てくる。80行目。ひとつのウィンドウを格子状のセルに分割して、以後に続くグラフ描画関数をどのセルに対して適用するかを指定する関数だ。3つの引数があって、第1と第2引数はそれぞれ何行、何列にウィンドウを分割するかを指定する。第3引数はグラフを描画するセルを指し示す数値だ。2行3列に分割した場合はこんな感じになる。
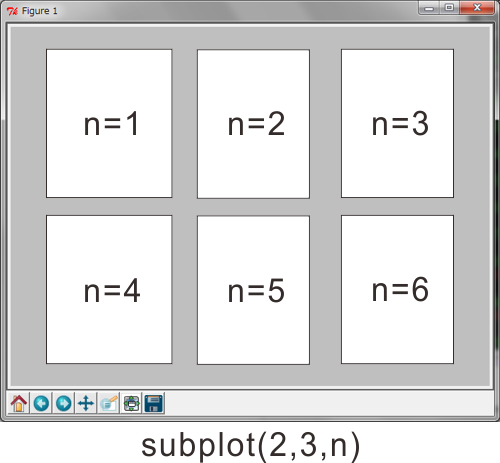
B: ふむふむ。
A: ちょっと注意が必要なのは、 pythonの慣例と異なり第3引数は0からではなく1から数え始める ということだ。恐らくこの関数がMatlabのsubplot()に由来しているからだと思うんだが、ここだけMatlab流に書かないといけないってのは鬱陶しい。80行目でもこの問題に対応するために1を足すということをしている。
B: AさんホントにMatlab嫌いですねえ。
A: んー。嫌いと言われると違う気がするな。あんなに価格が高くなければきっともっと愛していたと思うんだが。
B: 貧乏は人を歪めますねえ。
A: 金がないと心が荒むぞ。冗談じゃなく。とにかくpylab.subplot()の働きはわかってもらえたと思うんで、続いて83行目。
B: あ、ちょっと待ってください。
A: なんだ。今日はやけに止めるな。
B: 80行目のsubplot()の第3引数がよくわかりませんが…。
A: なんだ。ここはまるっきり例題14-2の応用だから説明不要かと思ったが。ここでは刺激の「手の左右」と「手の甲、手の平」の組み合わせ毎にグラフを描画しようとしている。2×2=4通りの組み合わせに1から4の番号を割り当てなければならない。あとは例題14-2を読み返すこと。いいな?
B: はーい。
A: さて、気を取り直して83行目。これは82行目から始まるpylab.plot()文の続きで、83行目では指定された「手の左右」、「手の甲、手の平」、「条件」の組み合わせにおける「手の回転角」別の反応時間の平均値を計算している。データが5次元のnumpy.ndarrayに格納されているので、ここに書かれているようにreactionTime[:,i,j,:,k]と書けば行方向に実験参加者、列方向に回転角が並んだ2次元配列を抜き出すことができる。ここも次元が増えているだけで例題14-2の14-2b.pyの83行目と同じ処理だから、わからなかったら例題14-2でやってるようにIPythonを使って確かめてみるといい。6次元、7次元とデータが複雑になろうとも、同じ方法でデータを抜き出すことができる。
B: もともとの例題14-2のケースでも同じ方法でいけるんですか。
A: うむ。大丈夫。
B: じゃあ例題14-2の方法はまったくの徒労じゃないですか。
A: そんなことはないぞ。ついさっき80行目のpylab.subplot()の第3引数を理解するときに使ったばかりじゃないか。それにpythonやMatlabのような配列操作が出来ない言語でプログラムを書かないといけなくなった時にこういうやり方を知らなかったら大変だ。
B: そんな機会はなさそうな気がするんですがねえ。
A: まあ、ないかも知れんがなあ。でもVisualBasicってどうなんだろ? VBAっていう形で結構使う機会があるんだが。今度ヒマがあったら確認しておくよ。
B: はい、そのまま忘れてしまうフラグ立ちましたー。
A: 後はテクニックというより単なる気配りだが、pylab.subplot()でずらっとグラフを並べると、どのグラフが何なんのかわからなくなってしまうことがよくある。そこで、75行目、76行目のようにラベル用文字列をリストにしておいて、86行目のようにグラフにタイトルをつける関数pylab.title()の引数lに指定しておく。するとこのようにそれぞれのグラフの上部にタイトルが付く。わかりやすいだろ?
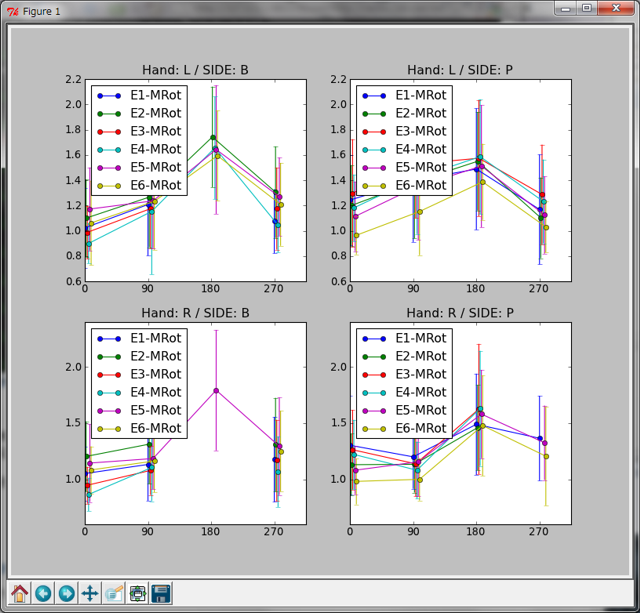
B: …。グラフのタイトルは確かにわかりやすいですが、縦軸の範囲が上下のグラフで違うのが気になりますね。それにグラフの凡例がグラフと重なって見難いです。
A: むむ、Bくんにそんな基本的なところでダメだしされるとは。今ぱぱっと修正するから待ってろ。それからあともうひとつ、気になるところがあるな。
B: 気になるところ?
A: なんだ。そっちは気づいていないのか。左下や右下のグラフをよく見てみなさい。グラフの線が欠けているだろ。
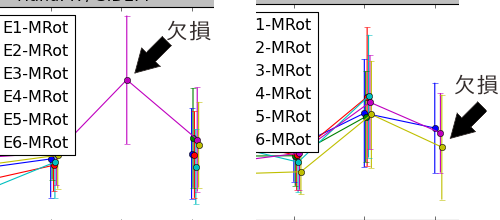
B: あ、ほんとだ。プログラムのミスですか?
A: いや、多分これはデータが欠損してるんだな。平均を計算する前のデータを確認してみるか。IPythonで14-3a.pyを実行して、えーっと、左下のグラフは「右手」の「手の甲」か。
In [3]: run 14-3a.py
In [4]: reactionTime[:,R,B,:,:]
Out[4]:
array([[[ 1.0545265 , 1.192407 , 0.78748233, 1.04239867, 1.23119283,
1.1474395 ],
[ 1.928003 , 1.439734 , 1.62371983, 1.29245983, 1.3989225 ,
1.5108916 ],
[ 1.680144 , 1.853795 , 1.6896306 , 1.901058 , 2.14409 ,
1.4501278 ],
[ 1.28553317, 0.961762 , 0.95669533, 0.84224483, 0.9022065 ,
1.14833667]],
[[ 1.0340275 , 1.50365417, 1.19797117, 1.00622517, 1.42864033,
(以下略)
B: うわ、すごい分量ですね。
A: ちょっと多かったか。じゃあ条件で絞るか。
In [5]: reactionTime[:,R,B,:,3]
Out[5]:
array([[ 1.04239867, 1.29245983, 1.901058 , 0.84224483],
[ 1.00622517, 1.17576633, 1.5742038 , 1.42860583],
[ 1.08958867, 1.42861317, 2.3111844 , 1.17293567],
[ 0.61177067, 0.9210445 , 1.4510125 , 0.760451 ],
[ 0.756209 , 1.067364 , NaN, 1.46475483],
[ 0.7227415 , 0.7038568 , 1.2466065 , 0.7138646 ],
[ 1.01867983, 1.24427783, 1.85926333, 1.059798 ],
[ 0.822814 , 0.90901683, 1.1606682 , 0.933973 ],
[ 0.81166633, 1.5508845 , 1.72876667, 0.91176733],
[ 1.11741633, 1.56757867, NaN, 1.9010626 ],
[ 0.81801883, 0.87694217, 1.64126725, 0.80147083],
[ 0.7799915 , 0.7838946 , 1.106489 , 0.8214165 ],
[ 0.77844467, 0.85046533, 1.26585867, 0.76170183],
[ 1.05548467, 1.748094 , 1.648819 , 1.17628233],
[ 1.00063533, 1.27021483, 1.90379333, 1.4814085 ],
[ 0.783893 , 1.01177783, 1.284106 , 0.9239614 ],
[ 0.7727675 , 1.05347517, 2.5429845 , 1.05068683],
[ 0.86172067, 0.86446967, 1.64818867, 1.3174914 ],
[ 0.68940567, 0.6872148 , 0.9895475 , 0.80336533],
[ 0.77277867, 1.10624217, 1.7176084 , 1.02568783]])
B: NaNっていうのがありますね。何ですか、これ?
A: NaNはnot a numberの略 で、0で割ろうとするなどして計算がエラーになった時に返される値だ。
B: 0で割るとエラーになるんですか?
A: あれ、小学校だか中学校だかで習わなかったか? 6÷3=2は3×2=6と書ける。同じように6÷0=aとすると0×a=6になってしまうからおかしいだろ。
B: あ、そうか。そういえば習ったような習わないような。
A: さて、この出力は1行目から順番に参加者01、参加者02、…に対応しているはずだから、 参加者05と10のデータに何か問題がある ってことだな。直接データファイルの中身を確認するか。被験者05、条件には3を指定したから対応するデータファイルはディレクトリs05のe04.txt。
B: 1ずれてるのがややこしいですねえ。
A: その辺は慣れるしかないな。さて、該当する条件は右手、手の甲、回転角180度だから、データファイル内では'R,B,180'という文字列が並んでいるはず。 エディタの検索機能で該当する行を抜き出してみるぞ。
R,B,180,1.367466,L
R,B,180,1.551026,L
R,B,180,2.267858,L
R,B,180,3.000000,-
R,B,180,3.000000,-
R,B,180,3.000000,-
A: 一番最初のL/Rが刺激で、一番最後のL/R/-が反応。両者が一致していれば正答。
B: 一問も正答していないですね。じゃあ平均反応時間がNaNになっていたのは…
A: 正答しなかった試行のデータは捨てているからな。全データが捨てられてしまったら平均を計算しようがないのは当たり前。 もっと試行数を増やせれば1回くらいは正答したかも知れないが、実験時間の都合上仕方がなかった。
B: 他の欠損も全部そうなんですか。
A: あー、多分そうだと思うが確認してない。B君、確かめておくこと!
B: ええっ、なんでぼくが。
A: うるさい。忙しいんだよ。これでも。
B: なんだかダメ人間っぷりが加速しているような。
A: それに予定以上に例題14-3も長くなってしまったから早く一区切りさせたい。
B: たった一言「そう」か「違う」かで答えれば済む話なのに…
A: とにかく欠損があるなら対処しないといけないな。B君ならどうする?
B: へっ? ええと、欠損がある参加者は分析から外す?
A: そうだな。最近はあまり推奨されないらしいが分析から外すのもひとつのやり方だな。じゃあ…、っっと、ちょっと待てよ。
B: どうしました?
A: いや、欠損のある参加者を探す方法にからんで、ちょっと教えておきたいことを思いついた。 そいつを話し出すと長くなるんで次回にまわすことにして、今回はNaNがあった場合は自動的に除外して平均や標準偏差を求める関数を紹介しておこう。scipy.statsをimportする。
B: scipy.stats? そんなの今までに出てきましたっけ。
A: え、scipyの紹介ってしてなかったか。ちょっと待てよ、grep、grep。
B: Aさん時々grepって言ってますけどソレ何ですか?
A: ん? Unix系OSでよくつかわれるテキスト検索コマンドだ。便利だぞ。…っと、scipyは例題10-3で名前が出てきただけか。 しまったな。scipyの解説もするとなるとさらに長い話になっちゃう。
B: なんだかAさん荒んでますし、ここでいったんお開きにします?
A: なんだ、B君に気を遣われると落ち着かないな。ごく簡単にだけ解説しておくよ。 まずscipyというのはpython上でさまざまな科学分野における計算処理を支援するパッケージだ。 Matlabで言うとSignal Processing、Optimization、StatisticsといったToolboxが提供する処理が含まれている。 まあ、私はMatlabのToolboxと比較してどちらがどの程度優れているとか言えるほど使い込んでいないんでアレなんだが、私程度の用途なら機能的にも速度的にもscipyで困ったことはない。
B: AさんAさん、それってAさんがどんな使い方してるのかわかんないと全然参考にならないと思うんですが。
A: む。確かに。まあその話はとにかく、scipyは巨大パッケージなので、一度にすべてimportしてしまうのではなく、いくつかの下位パッケージに分かれている。 その中で統計処理に関する関数が含まれているのがscipy.statsだ。
B: ふむふむ。
A: ま、正直なところscipy.statsに関してはMatlabのStatistics Toolboxの方がやや優れているかな、という気がしなくもないんだけど、混合計画の分散分析とかやろうとすると結局外部の統計パッケージに持ち込みたくなるんで50歩100歩だと思ってる。
B: scipy.statsって分散分析もできるんですか?
A: ScipyのDocumentsを見てくれ( Link )。結構いろいろ出来る。今回はそこまで解説する余裕はないんで、nanmeanとnanstdだけ。
B: はーい。
A: んじゃ、scipyをインストールしてない人は scipyのDownloadページ からダウンロードしてインストールしておいてください。そうそう、 scipyはインストールしているnumpyのバージョンに対応したものをインストールしないと動作しません 。特に Windows版バイナリでインストールする方でインストール済みのNumpyが1.3ならscipy0.7.1を入れる必要があります 。私はコレで嵌りました。
B: 毎度のことながらややこしいなあ。
A: まあこういうフリーのソフトウェアでは仕方がない事だと思う。特にscipyはいまだにversion 1に到達していない(2011年2月現在の最新版は0.9.0rc5)から、結構仕様が変わったりする。繰り返すけど仕方がないことだ。ついでに言っておくと、今回紹介するnanmean、nanstdは上記のDocumentsの最新版には載ってないんで今回の記事を書く前にちょっと焦ったんだけど、最新版のソースをダウンロードして確認したらちゃんと存在していたので安心した。こういうドキュメントの不備?も無いに越したことはないが、仕方あるまい。
B: ふーん。フリーってのも善し悪しだなあ。
A: 逆に言えば、有料のソフトウェアはこういう面倒事を販売元に解決してもらうために金を払ってるんだよ。時々有料なのにこの手の面倒事が生じるソフトウェアもあるけど。いや、時々じゃなくてしょっちゅうかな。
B: そんなのあるんですか。
A: いくらでもあるぞ。とにかく本題に戻ろう。scipyをインストールしたら、以下のプログラムをIPythonで実行してみてほしい。前回同様、まず14-3a.pyを実行してからrun -i 14-3b.pyとすること。
行番号なしのソースファイル→ 14-3b.py ※IPython上で14-3a.pyを実行した後に続けて-iオプション付きで実行します。
1import scipy.stats
2
3for i in range(nLR):
4 for j in range(nPB):
5 pylab.subplot(2,2,2*j+i+1)
6 for k in range(nCnd):
7 pylab.errorbar(pylab.arange(nDIR)+0.02*k, \
8 scipy.stats.nanmean(reactionTime[:,i,j,:,k],0), \
9 scipy.stats.nanstd(reactionTime[:,i,j,:,k],0), \
10 label=cndList[k],fmt='o-')
11 pylab.title('Hand: '+LRLabel[i]+' / SIDE: '+PBLabel[j])
12 pylab.xticks(pylab.arange(nDIR),DIRList)
13 pylab.ylim([0.6,2.6])
14 pylab.legend(loc='upper left',ncol=2)
15
16pylab.show()
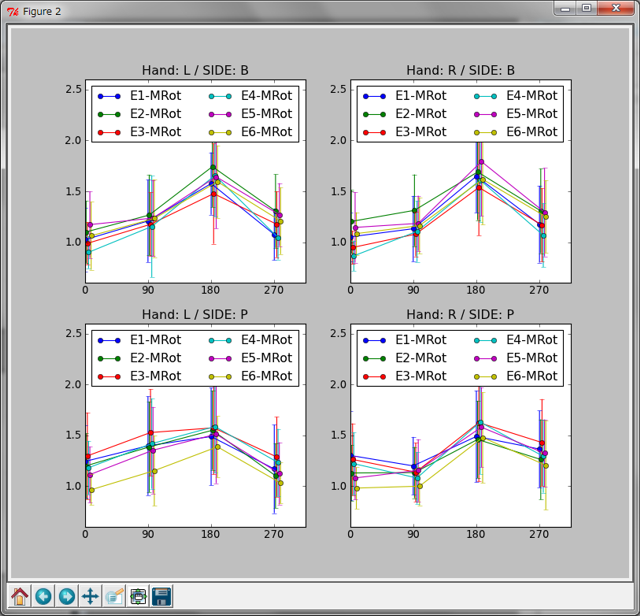
B: おお、ちゃんと欠けずに6本グラフが描かれてますね。
A: まあほとんど解説することもないんだが、1行目でscipy.statsをimport。 で、8行目と9行目のscipy.meanとscipy.stdがscipy.stats.nanmean、scipy.stats.nanstdに変更。以上。
B: へ? それで終わり? なにかこう、もっと解説することはないんですか?
A: そうだなあ。nanmeanとnanstdはそれぞれmeanとstdのNaNを無視してくれるバージョンとしか…。あ、そうそう。 pylab.stdではddofという引数に1を指定して不偏標準偏差を求めたが、scipy.stats.nanstdではbiasというオプションで指定する 。bias=Falseなら不偏標準偏差。bias=Trueなら標本標準偏差。省略時のデフォルト値はFalseだ。
B: 統一してくれたらいいのに。
A: まあそう言うな。後は細かい気遣いだが、グラフの配置が14-3a.pyと違っているのには気づいたか?
B: へ? そういえばそうですね。どうしたんですか?
A: 14-3a.pyのグラフだと2×2のグラフの上の行に左手、下の行が右手になってただろ。左手が左の列、右手が右の列になるように変更したんだ。5行目だね。やっぱりこういうのは対応しているのがわかりやすい。
B: Aさんてほんと気が利くんだか利かないんだかわかんない人ですね。そういえばグラフの凡例も変更されてますね。
A: 14-3a.pyの出力だと凡例がグラフに重なっていたから、凡例を2列にして重ならないようにした。14行目、pylab.legendのncol=2という引数だな。
B: まだエラーバーに重なってますが…。
A: うるさい。そして最後に13行目。pylab.ylimで縦軸の範囲を指定して、4つのグラフの縦軸を統一している。この辺りは前回B君に指摘されたところだな。
B: 一行書くだけなんですね。一行書くだけで全部のグラフの書式をまとめて変えられるってのは便利ですねえ。
A: うん。単発で1枚グラフを描くだけならExcelで済ませちゃうこともよくあるんだけど、同じフォーマットのグラフを数十枚も描くようなときは断然こっちのほうが楽だ。
B: さすがに何十枚もってもは大げさすぎでしょ。
A: そんなの研究内容によるぞ。それに学会発表や論文に使うかどうかは別として、個々の参加者のデータを確認するために数十人の参加者全員に対して同じフォーマットのグラフを描くこともある。
B: そんなもんですか。
A: 今回の例のように、全体の平均のグラフを描いて「あれっ?」と思った時とかな。いろんな実験をしているとそういう時もある。 さて、データ欠損のある参加者を除外する方法は次に回すことにしたから、例題14-3もそろそろおひらきかな。 例題14-4ではデータ欠損のある参加者の除外の方法と、他の統計パッケージで統計処理をするためのデータ出力について触れる。 それで例題14も締めくくりかな。
B: お疲れさまでしたー。
A: 最後に、没になったプログラムを例題14-3c.pyとして掲載しておこう。内容としては例題14-3b.pyと同じなんだが、横軸の270度の右に0度のデータをもう一度プロットして回転角度と反応時間の関係をわかりやすくしてある。 0度のデータを追加する部分がエレガントじゃないし、同じデータを一部だけ2回プロットするってのはあまりない処理なんで没にした。
B: 普段は「動けばいいんだよ!」とか言ってるくせにエレガントがどうとかこうとか。
A: まあまあ。でも、出力は14-3a.py、14-3b.pyよりずっとわかりやすいだろ?
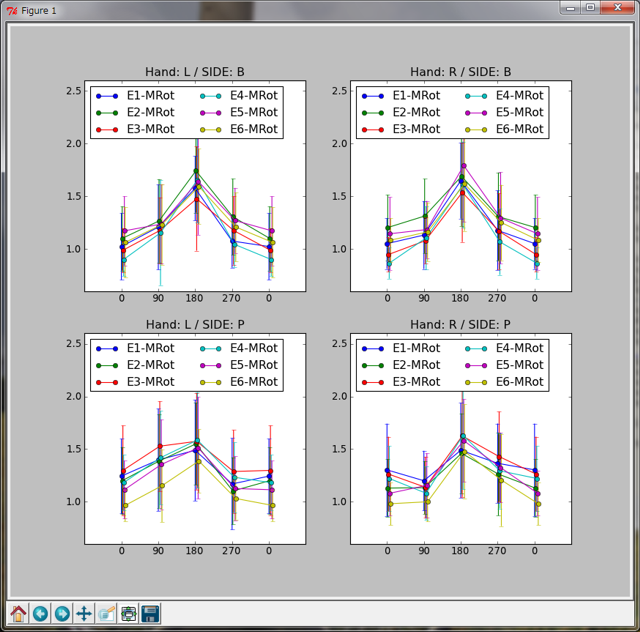
B: おお、確かにわかりやすい。こうやって見ると、上の段のグラフは両方とも左右対称っぽい感じがしますが、下の段のグラフは非対称ですね。 しかも鏡に映したように左右反転しているし。
A: 上の段は刺激が手の甲の写真、下の段は手の平の写真だな。エラーバーが長いんで微妙だが、交互作用があるかも知れんね。 プログラムで解説が必要な点があるとすればpylab.hstack(numpy.hstack)かな。引数に与えられたタプルの要素を横方向に連結したnumpy.ndarrayを作る関数だ。 要素の行数が合わないとエラーになる。縦方向に連結するにはnumpy.vstackという関数を使う。詳しくはIPythonでhelp hstackとかhelp.vstackしてほしい。 そんなわけで、次回に続きます。
行番号なしのソースファイル→ 14-3c.py ※IPython上で14-3a.pyを実行した後に続けて-iオプション付きで実行します。
1import scipy.stats
2
3for i in range(nLR):
4 for j in range(nPB):
5 pylab.subplot(2,2,2*j+i+1)
6 for k in range(nCnd):
7 m = scipy.stats.nanmean(reactionTime[:,i,j,:,k],0)
8 m = pylab.hstack((m,m[0]))
9 s = scipy.stats.nanstd(reactionTime[:,i,j,:,k],0)
10 s = pylab.hstack((s,s[0]))
11 xt = pylab.arange(nDIR+1)
12 xl = pylab.hstack((DIRList,DIRList[0]))
13 pylab.errorbar(pylab.arange(nDIR+1)+0.02*k, m, s, label=cndList[k],fmt='o-')
14 pylab.title('Hand: '+LRLabel[i]+' / SIDE: '+PBLabel[j])
15 pylab.xticks(xt,xl)
16 pylab.ylim([0.6,2.6])
17 pylab.legend(loc='upper left',ncol=2)
18
19pylab.show()