例題14-4:欠損をあしらう¶

A: B君、B君。作者からの差し入れをもらってきたから食べたまえ。

B: おっ、ずんだまんじゅうじゃないですか。僕、これ大好きです。豆っぽさがたまらない！いただきまーす。

A: なんだか知らないけど、作者が例題14-1から14-3を自分で読み返してへこんでいたよ。

B: むぐむぐ。むぁにがでふか？

A: 口いっぱいにほおばったまま喋るな。っていうか、その前にいっぺんに何個食べてんだ？

B: すゎんこでふ。むぐぅ。

A: 急がなくても私はもう先にいただいたから、ゆっくり食べたまえ。

B: はゎい。で、何でへこんでいたんですか。

A: いや、読み返したら会話がワンパターン化していて同じようなボケと突っ込みが連続していたり、「さて」とかが何度も続いていたりとかしているのに気付いて、自分の才能のなさを改めて思い知らされたらしい。

B: はあ。そんなんだったら会話形式やめりゃいいのにねえ。それとも気になる部分を書き直すか。

A: だな。私も「書き直せば？」って言ったんだが、講義期間が終わってさあ研究だ執筆だと思ったら仕事が山のように降ってきて大変らしい。で、例題14-4に何を書くつもりだったか忘れちゃいそうになってきたから修正より先に例題14-4を書いちゃいたいんだとさ。

B: なるほど。

A: さて、B君の腹ごしらえもひと段落ついたようだし、本題に入るか。今回は欠損値がある参加者を見つけるところからだな。前回から続きで読んでる人以外は、まず例題14-1の 14-1.zip をダウンロードして、展開してできたディレクトリに例題14-3の 14-3a.py を置いてIPythonからrun 14-3a.pyとして実行しておいてほしい。

B: ほいほい、ぼくはもうダウンロード済みなので…と、準備完了です。

A: では当面の目標だが、 データにまったく欠損がない参加者はTrue、ひとつでも欠損がある参加者はFalseになっているリスト を作りたい。今回のサンプルデータだと参加者が20名だから、参加者の順番にTrue、Falseが並んだ長さ20のリストになるな。このリストさえあれば、あとはnumpyの力で欠損がない被験者のデータだけを抜き取ることができる。

B: ふむふむ。

A: 実験条件にかかわらず、ひとつでも欠損があればアウトなので、データが要因別に多重配列になっている必要はない。扱いやすくするために、データの並べ方を変える。ここではreshapeというメソッドを用いる。

B: reshapeですか。そのまんまの名前ですね。

A: まず、反応時間のデータが格納されている変数reactionTimeの配列の構造を確認しておこう。numpy.ndarray型の配列はshapeというデータ属性を持っていて、ここに配列の構造を示すタプルが保持されている。

In [33]: reactionTime.shape
Out[33]: (20, 2, 2, 4, 6)

B: 5次元の配列ですね。

A: これをreshapeを使って1人の参加者のデータがずらっと1行に並ぶ2次元の配列に変換する。reshapeは引数に「どのような形の配列に変形したいのか」を示すタプルを指定する。今の場合だと20行、…ええと、何列だ。2×2×4×6列の行列に変換したいので、以下のように指定する。

In [34]: reactionTime.reshape((20,2*2*4*6))
Out[34]:
array([[ 1.18823217,  1.250766  ,  1.08383367, ...,  1.76767367,
         1.25095667,  1.10626417],
       [ 0.93952   ,  1.292444  ,  1.2174168 , ...,  1.9644274 ,
         1.9477354 ,  1.8732465 ],
       [ 1.520351  ,  1.54530083,  1.23136783, ...,  1.2941048 ,
         1.530875  ,  1.20630617],
       ...,
       [ 0.72280733,  1.00067367,  0.867246  , ...,  1.20978233,
         1.4925425 ,  1.6309248 ],
       [ 0.75611083,  0.76722483,  0.681062  , ...,  0.78391925,
         1.06461617,  0.7672152 ],
       [ 0.86446417,  0.917259  ,  0.84503667, ...,  1.00620783,
         1.59534583,  1.1674435 ]])

B: Aさん、2×2×4×6は96ですよ。

A: おお、ありがとう。私ぁ暗算は大の苦手なんだ。B君の答えを疑うわけじゃないが、pythonでも確認しておこう。reshapeの戻り値はnumpy.ndarray型はので、そのまま最後に.shapeをくっつけたら変換後の配列の構造を示すタプルが得られる。

In [35]: reactionTime.reshape((20,2*2*4*6)).shape
Out[35]: (20, 96)

B: 20行96列の2次元配列ですね。それにしてもこの最後に.shapeってつける書き方は何度見ても気持ち悪いなあ。

A: そうかね。私なんかは逆にこういう書き方をさせてくれない言語の方が使っていてイライラしてくるが。とにかく、reshapeは変換前と変換後の要素数が一致しなければエラーになる。当然のことだね。

B: 当然、ですか？

A: そうだろ。変換後に要素数が減るんならどの要素を捨てるんだってことになるし、変換後に増えるんならどんな値をどこに増やすんだってことが問題になる。

B: ああ、そうか。

A: ちなみに、変換後の配列がn次元の場合、n-1個の次元について指定してしまえば残りの一次元は「要素数が変わらない」という制限から決まってしまう。例えば今回の場合、変換後が2次元で最初の次元の要素数が20なんだから、もう一つの次元の要素数は96以外にありえない。そこで、reshapeの引数のタプルにひとつだけ-1が含まれている場合、reshapeが自動的に-1を指定された次元の要素数を計算してくれる。

B: ？

A: つまり、このように書いたら自動的に20行96列に変換してくれるということだ。

In [36]: reactionTime.reshape((20,-1)) #次元のひとつは-1を指定できる

B: なるほど。こりゃ便利ですね。-1はひとつだけしか使えないんですか…って、そりゃそうか。ふたつあったらどういう構造に変形するのか特定できないもんな。

A: 自己解決したな。よしよし。ついでに少し補足しておくと、reshapeはタプルではなく複数の整数を引数として並べてもタプルを指定した時と同様の結果が得られる。それから、numpy.ndarrayのメソッドとしてではなく、普通の関数としてもreshapeは用意されている。関数のreshapeの場合は第一引数に変換元のnumpy.ndarray型配列、第二引数に変換後の構造を示すタプルをしていする。この場合は複数の引数を並べる方法はダメで、かならずタプルを用いなければならない。

In [37]: reactionTime.reshape(20,-1) #tupleでなくてもよい
In [38]: pylab.reshape(reactionTime,(20,-1)) #この場合はtupleじゃないとダメ

B: ややこしいなあ。統一してくれればいいのに。

A: 私はどちらの場合でもタプルで書くことにしてるけどね。 B: ところでこの96列の方はどういう順番に並んでいるんですか？

A: ああ、それは欠損の検出では問題にならないんで、データをファイルに出力するときに改めて説明するよ。さて、…と。話の続きを始める前に、これから先の流れをまず書いておいた方がわかりやすいかな。

各参加者のデータを1行にまとめる

NaNの要素を見つける

NaNがひとつでも含まれる被験者を見つける

A: 今、reshapeで第一段階はクリアした。続いてNaNである要素を見つけよう。これにはpylab.isnanという関数を用いる。まあもともとはnumpy.isnanなんだが前にも言ったけどこの例題ではpylabをimportしているんで全部pylabで統一しておく。

In [39]: pylab.isnan(reactionTime.reshape((20,-1)))
array([[False, False, False, ..., False, False, False],
       [False, False, False, ..., False, False, False],
       [False, False, False, ..., False, False, False],
       ...,
       [False, False, False, ..., False, False, False],
       [False, False, False, ..., False, False, False],
       [False, False, False, ..., False, False, False]], dtype=bool)

B: 戻り値はFalseばっかりですね。

A: Trueだったらそこの要素はNaN、つまりデータが欠損しているということだからな。Trueがうじゃうじゃあったら困る。こういう風にしてしまうと全参加者のデータに対する判定結果が出力されてしまうので、特定の被験者を抜き出してみようか。ええと、確か参加者s05は欠損があったんだよな。ということは0から数えるから4番の被験者のデータには欠損があるはず。そりゃ。

In [40]: isnan(reactionTime.reshape((20,-1)))[4]
Out[40]:
array([False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False,  True, False,
        True, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False, False, False, False, False, False, False, False, False,
       False,  True, False, False, False, False], dtype=bool)

B: isnan(ほにゃらら)の後に[4]と続くのが気持ち悪い…。isnanの戻り値がnumpy.ndarrayだからこういうことが出来るんですよね。

A: 気持ち悪ければ、自分で作業するときは変数に一度代入したまえ。とにかく、予想通りTrueが含まれているな。

B: Trueが3つありますね。3つの条件で欠損していたと理解すればいいんですかね。

A: そういうことだな。さて、ここにひとつでもTrueが含まれているかを判定するにはどうしたらいい？

B: ふふっ、自信ありますよ。True in isnan(ほにゃらら)でばっちり！

A: …。

B: あ、あれ、外しました？

A: いや、それでもいいんだが、ここはnumpy流に行こうか。numpy.ndarrayには要素にひとつでもTrueが含まれているときにTrue、それ以外の時にFalseを返すanyというメソッドがある。anyはreshapeと同様に、numpy.ndarrayのメソッドとしても使えるし、関数としても使える。

In [41]: isnan(reactionTime.reshape((20,-1)))[4].any()
Out[41]: True

B: まだ教えてもらってない方法を聞くなんて、そんなのわかるわけないじゃないですか。ずるい！

A: すまん、すまん。つい成り行きで聞いてしまった。in演算子を覚えていたのは偉かったぞ。4番の参加者に対するisnanの結果にはTrueが含まれているので、any()の戻り値はTrue。isnanの結果がすべてFalseの場合は…、と。0番の被験者はすべてFalseのようだから、0番の被験者でやってみよう。

In [42]: isnan(reactionTime.reshape((20,-1)))[0].any()
Out[42]: False

B: 戻り値はFalseですね。

A: わかったかな。これでデータにひとつでもNaNを含む参加者とひとつも含まない参加者に対してそれぞれTrue、Falseを割り当てることができる。ただ、今回は逆にNaNを含む参加者に対してFalse、含まない参加者に対してTrueを割り当てないといけないので、もうひとひねり必要だ。

B: ちょ、ちょっとわけがわからなくなってきました。

A: ちなみにanyに似たメソッドでallというメソッドもある。こちらはすべての要素がTrueならTrue、ひとつでもFalseがあればFalseだ。

In [43]: isnan(reactionTime.reshape((20,-1)))[4].all()
Out[43]: False

In [44]: isnan(reactionTime.reshape((20,-1)))[0].all()
Out[44]: False

B: なるほど、このallを使えば問題解決！！ …って、あれ？どう使ってもうまくいかないな。あれ？

A: allは単にanyを紹介したついでに紹介しただけだから。今回の場合はallを使ってもうまくいかないよ。

B: がっくり。だまされた…

A: 別にだましちゃいないが。anyの戻り値がFalseならTrue、TrueならFalseが得られればいいんだから、あまりスマートじゃないが、こうすればいい。

In [45]: isnan(reactionTime.reshape((20,-1)))[4].any()==False
Out[45]: False

In [46]: isnan(reactionTime.reshape((20,-1)))[0].any()==False
Out[46]: True

B: あ…なるほど。Falseと等しいか評価すればいいんですね。

A: あるいはこういうやりかたもある。この場合はanyではなくallを使う。

In [47]: tmp = reactionTime.reshape(20,2*2*4*6)

In [48]: (tmp==tmp)[4].all()
Out[48]: False

In [49]: (tmp==tmp)[0].all()
Out[49]: True

B: ？？？ tmpとtmpが等しい？そんなの必ずTrueじゃないんですか？

A: 意味わかんないよな。私も最初面食らったんだが、 pythonではNaNとNaNの比較はFalseになるんだ 。もちろん普通の数値の場合はTrueになるんで、 tmp==tmpとすればisnan(tmp)とは逆にNaNのところだけFalse、その他はTrueという戻り値が得られる 。

B: えー。気持ち悪い。

A: これに関しては「気持ち悪い」に同意。気持ち悪いって言うか、直感的じゃないよな。でもこれ、結構便利なんで私はちょくちょく使っている。まあ前の例のようにFalseと比較する方が可読性が高いプログラムだろうな。

B: Aさんのチョイスがよくわからないなあ。読みやすさ重視なのか、そうじゃないのか。

A: 単に最初に思いついた方法を使い続けているだけだな。とにかく、これで「NaNがひとつでも含まれる被験者を見つける」という目標も達成だ。後は参加者順にリストにまとめるだけ。さて、B君ならどうする？

B: ええと、…

A: っと。またまだ教えていない方法を質問してB君に怒られるところだった。すまんすまん。

B: へ？またですか？

A: うん。多分こんな感じのfor文を組もうと思っただろ？

[pylab.isnan(reactionTime.reshape((20,-1)))[i].any()==False
    for i in range(reactionTime.shape[0])]

B: …forは使おうと思いましたが1行で書こうとは思いませんでした。

A: あらら。そうか。でもfor文を使うというのは今まで教えてきた方法の中では自然な発想だよな。

B: 他に方法があるんですか？

A: pylab(numpy)にapply_along_axisという関数があるんだ。apply_along_axisの第1引数で指定した関数を、第2引数で指定した軸に沿って第3引数で指定した配列に適用する。

In [50]: pylab.apply_along_axis(any,1,isnan(reactionTime.reshape((20,-1))))
Out[50]:
array([False,  True, False, False,  True,  True, False, False,  True,
        True, False, False, False,  True, False, False,  True, False,
       False, False], dtype=bool)

B: ？？？軸？に沿って…？

A: ちょっと解説が必要かな。実はaxisという概念は平均を計算するmeanや標準偏差を計算するstdを紹介した時にすでに出てきているんだが、あの時はちゃんと説明しなかった。この例を見てみてほしい。まず適当な2次元の行列を準備する。

In [51]: x = pylab.arange(24).reshape(4,6)

In [52]: x
Out[52]:
array([[ 0,  1,  2,  3,  4,  5],
       [ 6,  7,  8,  9, 10, 11],
       [12, 13, 14, 15, 16, 17],
       [18, 19, 20, 21, 22, 23]])

In [53]: x[2,4]
Out[53]: 16

B: へ？これが何か？

A: 続いてaxisを指定してmeanを適用する。axisに指定した値と平均を計算する方向の関係がわかるかな？

In [54]: pylab.mean(x,axis=0)
Out[54]: array([  9.,  10.,  11.,  12.,  13.,  14.])

In [55]: pylab.mean(x,axis=1)
Out[55]: array([  2.5,   8.5,  14.5,  20.5])

B: ええと、axis=0なら縦方向。axis=1なら横方向。

A: ふむ。縦、横じゃなくて列、行と言ってほしかったところだが。で、なぜそうなるかわかるかな？

B: へ？なぜって言われても…

A: さっきx[2,4]が16になるって示しておいたのは重要な意味があるんだ。x[ ]の中の0番目の数は何行目かを示していて、1番目の数は何列目かを示しているということはわかるか。

B: はあ、それはわかります。

A: 図に描くとこんな感じだな。

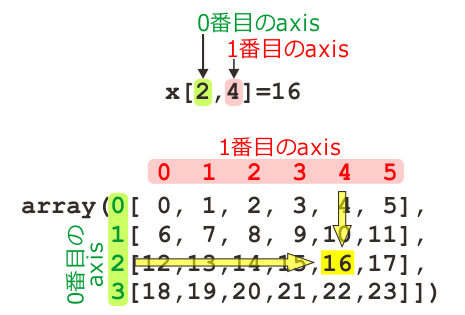
B: いくらなんでもこのくらい図を描いてくれなくてもわかりますが。

A: まあそう言うな。ここで大事なのは、x[ ]の中の0番目の数字はこの図では「縦軸」に沿って、1番目の数字は「横軸」に沿って並んでいるということだ。

B: ああ！なるほど。ということは…

A: そう。0番目の数字は縦軸に沿って並んでいるんだから、0番目の軸は縦軸。同様に1番目の軸は横軸。で、meanのオプション引数axisはどの軸に沿って平均を計算するかを指定してするんだから、axis=0を指定すると縦方向に平均を計算する。

B: で、axis=1なら横方向に計算した結果になるんですね。

A: その通り。重要なことは、ここで縦とか横とか言っているのは2次元の配列を第0軸が縦、第1軸が横になるように図示しているからそうなるだけで、平面図には簡単に表現できないような5次元、6次元の配列でも同様に考えることが出来るということだ。

B: 同じように…？？どんな図になるんだろう。

A: 3次元以上の場合は図にしようとするとかえってわかりにくくなるかも知れんね。言い方を変えると、軸に沿って平均を計算すると、引数に指定した軸が失われた1次元小さい配列が戻り値として得られる。上の例なら、(4,6)というshapeの2次元配列の第0軸に沿って平均を計算すると戻り値は要素数6の1次元配列。第1軸だと要素数4の1次元配列。いずれも元の2次元配列より1次元小さくなっていて、その要素数は指定しなかった方の軸の要素数と一致している。

B: うむむ～。

A: 5次元の場合も同様で、軸に沿って平均を計算すると、戻り値は4次元の配列となる。で、その要素数はやはり元の配列から指定した軸を落としたものになっている。

B: むはっ、戻り値の配列が具体的にどんな配列になるのか見当がつきません。

A: まあ、実際に多次元の配列を作ってaxisをいろいろ変えて計算してみるといいよ。あと、第1引数に与える関数は何でもいいわけじゃないので、詳しくはhelp apply_along_axisしてみてほしい。さて、じゃあ改めて聞くけど、今回のデータでは第0軸に参加者、第1軸に実験条件が並んでいる。各参加者について、ひとつでもTrueがあるかどうかを判定するには、anyをどちらの軸に沿って適用したらいい？

B: 第1軸ですね。

A: ご名答。meanならばオプション引数axisを指定すればこういった軸に沿った計算が簡単に出来るわけだが、もちろんaxisオプションに対応していない関数もたくさんある。そういった関数を軸に沿って適用したい場合はこのapply_along_axisが役に立つ。

B: なるほどなるほど。じゃあanyはaxisオプションがない関数なんですね？

A: いや、ある。

B: ！！(激しくずっこける) じゃあaxisオプションを使えばいいじゃないですか！

A: うむ。まあ確かにその通りなんだが、前回「教えておきたいことを思いついた」って言っただろ？ numpyを使いこなすうえでaxisの考え方は重要なんだが、今までロクに説明せずになんとなくmeanやstdで使っていたからな。ここでちゃんと図を使って説明しておきたかった。

B: む、そう言われるともっともらしいような、でもAさんのことだからもっとおっちょこちょいだったり行き当たりばったりする理由のような…

A: 疑り深い奴だな。あと、今回は詳しく解説しないけど複数の軸に対して関数を適用するapply_over_axesという関数もあるんで、これもhelpで調べておいてほしい。こちらは正真正銘meanやstdのaxisオプションでは対応できない処理だ。

B: なんだか「help見てください」ばっかりになってきたなぁ。

A: さて、これで目的の「データにまったく欠損がない参加者はTrue、ひとつでも欠損がある参加者はFalseになっているリスト」を作る準備はすべて整った。まずはisnanとanyを使ってひとつでも欠損がある参加者を見つけてからFalseと比較してTrueとFalseをひっくり返す方法。

In [56]: pylab.apply_along_axis(any,1,isnan(reactionTime.reshape((20,-1))))==False
Out[56]:
array([ True, False,  True,  True, False, False,  True,  True, False,
       False,  True,  True,  True, False,  True,  True, False,  True,
        True,  True], dtype=bool)

A: apply_alogn_axisを使わずにanyのaxisオプションを使うならこうだ。出力が一緒になることを確認してほしい。

In [57]: isnan(reactionTime.reshape((20,-1))).any(axis=1) == False
Out[57]:
array([ True, False,  True,  True, False, False,  True,  True, False,
       False,  True,  True,  True, False,  True,  True, False,  True,
        True,  True], dtype=bool)

B: 確かに同じですね。ええと、Falseの人は7人。20人中7人がどこかで欠損データがあるのか。

A: 最後にNaN==NaNがFalseになることを利用する方法。これも同じ結果になる。

In [58]: tmp = reactionTime.reshape((20,-1))

In [59]: (tmp==tmp).all(axis=1)
Out[59]:
array([ True, False,  True,  True, False, False,  True,  True, False,
       False,  True,  True,  True, False,  True,  True, False,  True,
        True,  True], dtype=bool)

B: さて、じゃあいよいよデータをファイルに出力して例題14もおしまいですね。いやあ、長かったなあ。

A: いや、その通りなんだが、思ったより解説が長くなってしまったんでここで一区切りさせてくれ。ファイルへの出力は例題14-5ということで。

B: えぇ？！また先延ばしですか？

A: うん。本当は2、3回くらいでぱぱっと済ませるつもりだったんだが、話していくうちに「ああ、これも説明しとかなきゃな。あれも、それも。」ってな具合にずいぶん長くなってしまった。今度また「次回に続く」にしちゃったらひとつの例題の最長記録更新になっちまうから、次回は何としても終わらせるぞ。

B: 別に更新しても何も問題ないような気がしますが…。

A: うるさい。というわけで、次回に続く。B君、食べ散らかしたまんじゅうの包み紙を片づけておくこと。

B: へーい。

例題14-4:欠損をあしらう¶

十河研究室

目次

Related Topics